Linear model with many regressors
03 January, 2023
Overview
Ridge regression
We try to minimize
\[ \sum_{i=1}^n \Big( Y_i - X_i \beta \Big)^2 + \lambda \sum_p \beta_p^2 \]
checking the bias and variance
When looking at
set.seed(43215)
# let's consider a simple model with p independent regressors
p = 10
beta = rev(sort(rnorm(p)))
n = 20
p2 = 18
# let's regularize it
rr = data.table( foreach (lambda = seq(0,5,l=20),.combine=rbind) %:% foreach (i = 1:500,.combine=rbind) %do% {
X = array(rnorm(p2*n),c(n,p2));
Y = X %*% c(beta,rep(0,p2-p)) + sigma*rnorm(n)
fit = lm.ridge(Y~0+X,lambda=lambda)
res = data.frame(value=coef(fit),value0=c(beta,rep(0,p2-p)))
res$rep = i
res$name = rownames(res)
res$lambda = lambda
res
})
rs = rr[,list(bias=mean(value-value0)^2,var=var(value-value0),mse=mean((value-value0)^2)),list(name,lambda)]
ggplot(rs[name=="X1"],aes(x=lambda,y=mse)) + geom_line() + theme_bw() +
geom_line(aes(y=bias),color="red") + geom_line(aes(y=var),color="blue") + # scale_y_log10() +
geom_vline(xintercept = rs[name=="X1"][which.min(mse),lambda],linetype=2)
ls = unique(rr$lambda)[c(1,5,10,15)]
ggplot(rr[name=="X1"][lambda %in% ls],aes(x=value, group=lambda,fill=lambda,color=lambda)) +
geom_density(alpha=0.3) + geom_vline(xintercept = beta[1],linetype=2) + theme_bw() + xlim(-1,3)## Warning: Removed 76 rows containing non-finite values (`stat_density()`).
# looking at the results in this case - extracting the best lambda
r2 = rs[name %in% paste("X",1:p,sep=""),mean(mse),lambda]
lambda_star = r2[,{I=which.min(V1);lambda[I]}]
beta0 = c(beta,rep(0,p2-p))
Y = X %*% c(beta,rep(0,p2-p)) + sigma*rnorm(n)
# ridge at best lambda
fit = lm.ridge(Y~0+X,lambda=lambda_star)
# OLS
fit2 = lm.ridge(Y~0+X,lambda=0)
# remove noise to get the truth
Y = X %*% c(beta,rep(0,p2-p))
fit3 = lm(Y~0+X)
# combine results
rr2 = rbind(
data.frame(as.list(coef(fit)),name="ridge"),
data.frame(as.list(coef(fit2)),name="ols"),
data.frame(as.list(coef(fit3)),name="true"))
rr2$name = paste(rr2$name)
# melt to plot
rr3 = melt(rr2,id.vars = "name")
rr3$var = as.integer(str_replace(rr3$variable,"X",""))
ggplot(rr3,aes(x=var,y=value,color=name)) + geom_point() + geom_line() + theme_bw()
Running cross-validation
X = array(rnorm(p2*n),c(n,p2));
Y = X %*% c(beta,rep(0,p2-p)) + sigma*rnorm(n)
# compute the Lasso with cross-validation
cvfit <- glmnet::cv.glmnet(X, Y,alpha=0,intercept=FALSE)## Warning: Option grouped=FALSE enforced in cv.glmnet, since < 3 observations per
## foldcvfit$lambda.min## [1] 0.5048955plot(cvfit)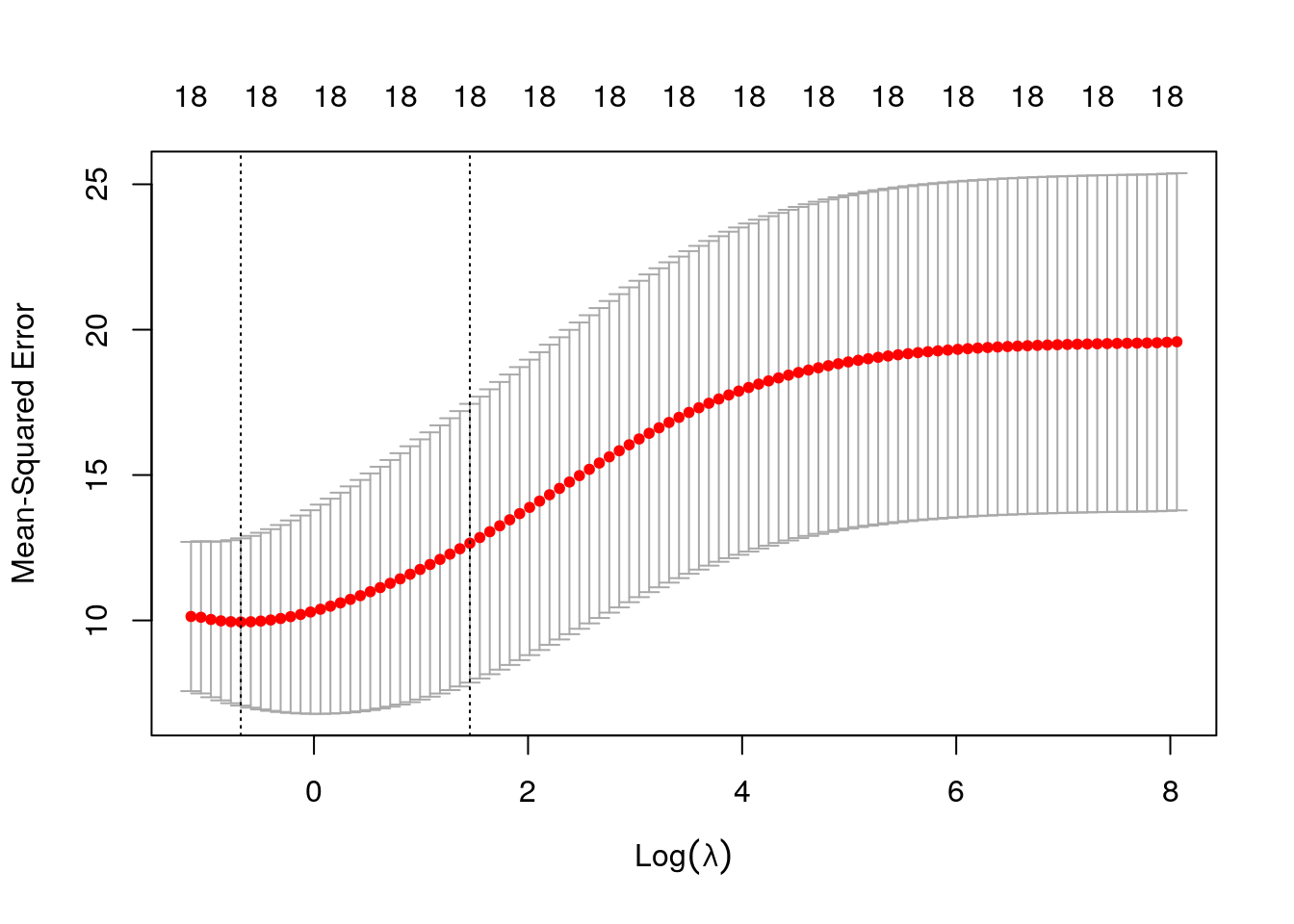
coef(cvfit)## 19 x 1 sparse Matrix of class "dgCMatrix"
## s1
## (Intercept) .
## V1 0.67752150
## V2 0.09009910
## V3 -0.17655263
## V4 -0.45634145
## V5 -0.13428149
## V6 -0.22334881
## V7 -0.01340456
## V8 -0.95156884
## V9 -1.43552174
## V10 -0.66430589
## V11 0.54981918
## V12 0.22399210
## V13 0.09838902
## V14 -0.26864706
## V15 0.22493636
## V16 0.27324261
## V17 -0.12062688
## V18 -0.53592517Lasso
We now minimize
\[ \sum_{i=1}^n \Big( Y_i - X_i \beta \Big)^2 + \lambda \sum_p | \beta_p | \]
# compute the Lasso with cross-validation
cvfit <- glmnet::cv.glmnet(X, Y)## Warning: Option grouped=FALSE enforced in cv.glmnet, since < 3 observations per
## fold# attach the results
rr2 = rbind(rr2,rr2[1,])
rr2[4,1:p2] = as.matrix(coef(cvfit, s = "lambda.1se"))[2:(p2+1)]
rr2$name[4] <- "lasso"
rr3 = data.table(melt(rr2,id.vars = "name"))
rr3 <- rr3[,var:= as.integer(str_replace(rr3$variable,"X",""))]
ggplot(rr3,aes(x=var,y=value,color=name)) + geom_line() + theme_bw() +geom_point()
Applying to Hitter database
Borrowed from the book ISLR, Chapter 6 Lab 2: Ridge Regression and the Lasso
library(ISLR)
# remove NA
Hitters = Hitters[!is.na(Hitters$Salary),]
library(corrgram)
corrgram(Hitters, order=TRUE, lower.panel=panel.shade,
upper.panel=panel.pie, text.panel=panel.txt)
# prepare the data for glmnet
x=model.matrix(Salary~.,Hitters)[,-1]
y=Hitters$SalaryRidge Regression
# prepare a grid for lambda
grid=10^seq(10,-2,length=100)
ridge.mod=glmnet(x,y,alpha=0,lambda=grid)
# dim(coef(ridge.mod)) # coef is 20x100
coefs = t(as.array(coef(ridge.mod)[,seq(1,100,11)]))
dt = data.table(coefs)
dt$lambda = log(ridge.mod$lambda[seq(1,100,11)])/log(10)
knitr::kable(dt,digits = 4) %>%
kable_styling(bootstrap_options = c("striped", "hover", "condensed","responsive"), full_width = F)| (Intercept) | AtBat | Hits | HmRun | Runs | RBI | Walks | Years | CAtBat | CHits | CHmRun | CRuns | CRBI | CWalks | LeagueN | DivisionW | PutOuts | Assists | Errors | NewLeagueN | lambda |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 535.9257 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 10.0000 |
| 535.9218 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | -0.0002 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 8.6667 |
| 535.8383 | 0.0000 | 0.0001 | 0.0004 | 0.0002 | 0.0002 | 0.0002 | 0.0008 | 0.0000 | 0.0000 | 0.0001 | 0.0000 | 0.0000 | 0.0000 | -0.0003 | -0.0036 | 0.0000 | 0.0000 | 0.0000 | -0.0001 | 7.3333 |
| 534.0450 | 0.0005 | 0.0020 | 0.0079 | 0.0033 | 0.0035 | 0.0041 | 0.0169 | 0.0000 | 0.0002 | 0.0013 | 0.0003 | 0.0004 | 0.0004 | -0.0057 | -0.0780 | 0.0002 | 0.0000 | -0.0002 | -0.0011 | 6.0000 |
| 497.8943 | 0.0110 | 0.0401 | 0.1591 | 0.0676 | 0.0711 | 0.0842 | 0.3384 | 0.0009 | 0.0035 | 0.0261 | 0.0069 | 0.0072 | 0.0075 | -0.0799 | -1.6419 | 0.0045 | 0.0007 | -0.0040 | 0.0065 | 4.6667 |
| 181.6207 | 0.0976 | 0.4148 | 1.2512 | 0.6587 | 0.6495 | 0.8612 | 2.6285 | 0.0083 | 0.0322 | 0.2386 | 0.0646 | 0.0669 | 0.0632 | 4.4262 | -25.8850 | 0.0611 | 0.0084 | -0.1931 | 3.7980 | 3.3333 |
| 21.2475 | -0.1144 | 1.3889 | -0.7097 | 1.1635 | 0.8456 | 2.1867 | -2.8561 | 0.0094 | 0.0821 | 0.5385 | 0.1656 | 0.1754 | -0.0418 | 36.7654 | -108.6578 | 0.2275 | 0.0769 | -2.6306 | 0.0068 | 2.0000 |
| 147.0439 | -1.5738 | 5.4959 | 0.5084 | -0.2529 | 0.1039 | 5.1516 | -10.4583 | -0.0532 | 0.2007 | 0.7266 | 0.6772 | 0.3600 | -0.5943 | 61.2550 | -122.8933 | 0.2791 | 0.2856 | -3.7768 | -27.7553 | 0.6667 |
| 164.4100 | -1.9655 | 7.2719 | 3.5682 | -2.0162 | -0.7999 | 6.1424 | -4.5520 | -0.1618 | 0.2187 | 0.1757 | 1.2893 | 0.6530 | -0.7818 | 63.2964 | -117.6506 | 0.2822 | 0.3666 | -3.4563 | -26.4182 | -0.6667 |
| 164.1132 | -1.9739 | 7.3777 | 3.9366 | -2.1987 | -0.9162 | 6.2004 | -3.7140 | -0.1751 | 0.2113 | 0.0563 | 1.3661 | 0.7097 | -0.7958 | 63.4049 | -117.0824 | 0.2820 | 0.3732 | -3.4240 | -25.9908 | -2.0000 |
Using cross-validation with training and testing sets
# split the sample in 2
set.seed(1)
train=sample(1:nrow(x), nrow(x)/2)
test=(-train)
y.test=y[test]
# compute the ridge regression usign the train data
ridge.mod=glmnet(x[train,],y[train],alpha=0,lambda=grid, thresh=1e-12)
# compute the MSE on the test data for s=4
dd = data.frame()
for (l in grid) {
cc = predict(ridge.mod,s=l,newx=x[test,],type = "coefficients")
cmse = sum(cc[2:20,]^2)
ridge.pred=predict(ridge.mod,s=l,newx=x[test,])
v1=mean((ridge.pred-y.test)^2)
y.train=predict(ridge.mod,s=l,newx=x[train,])
v2=mean((y[train]-y.train)^2)
dd = rbind(dd,data.frame(i=i,l=l,test=v1,train=v2,cmse=cmse))
}
ggplot(dd,aes(x=l,y=test)) + geom_line() + scale_x_log10()
ggplot(dd,aes(x=l,y=train)) + geom_line() + scale_x_log10()
ggplot(dd,aes(x=l,y=cmse)) + geom_line() + scale_x_log10()
# compare the MSE for Rdige to mse for OLS
ridge.pred=predict(ridge.mod,s=0,newx=x[test,])
mean((ridge.pred-y.test)^2)## [1] 167789.8lm(y~x, subset=train)##
## Call:
## lm(formula = y ~ x, subset = train)
##
## Coefficients:
## (Intercept) xAtBat xHits xHmRun xRuns xRBI
## 274.0145 -0.3521 -1.6377 5.8145 1.5424 1.1243
## xWalks xYears xCAtBat xCHits xCHmRun xCRuns
## 3.7287 -16.3773 -0.6412 3.1632 3.4008 -0.9739
## xCRBI xCWalks xLeagueN xDivisionW xPutOuts xAssists
## -0.6005 0.3379 119.1486 -144.0831 0.1976 0.6804
## xErrors xNewLeagueN
## -4.7128 -71.0951predict(ridge.mod,s=0,type="coefficients")[1:20,]## (Intercept) AtBat Hits HmRun Runs RBI
## 274.2089049 -0.3699455 -1.5370022 5.9129307 1.4811980 1.0772844
## Walks Years CAtBat CHits CHmRun CRuns
## 3.7577989 -16.5600387 -0.6313336 3.1115575 3.3297885 -0.9496641
## CRBI CWalks LeagueN DivisionW PutOuts Assists
## -0.5694414 0.3300136 118.4000592 -144.2867510 0.1971770 0.6775088
## Errors NewLeagueN
## -4.6833775 -70.1616132# use the library cross-validation
set.seed(1)
cv.out=cv.glmnet(x[train,],y[train],alpha=0)
plot(cv.out)
# get best lambda
bestlam=cv.out$lambda.min
bestlam## [1] 326.0828# compute MSE at best
ridge.pred=predict(ridge.mod,s=bestlam,newx=x[test,])
mean((ridge.pred-y.test)^2)## [1] 139856.6ridge_best = glmnet(x,y,alpha=0,lambda = bestlam)
ridge_best = predict(ridge_best,type="coefficients",s=bestlam)[1:20,]The Lasso
# plot coefficients for all values of lambda
lasso.mod=glmnet(x[train,],y[train],alpha=1,lambda=grid)
plot(lasso.mod)## Warning in regularize.values(x, y, ties, missing(ties), na.rm = na.rm):
## collapsing to unique 'x' values
# plot the MSE for all coefficients
cv.out=cv.glmnet(x[train,],y[train],alpha=1)
plot(cv.out)
# extract the best lambda in terms of cross-validation
bestlam=cv.out$lambda.min
lasso.pred=predict(lasso.mod,s=bestlam,newx=x[test,])
# compute the MSE
mean((lasso.pred-y.test)^2)## [1] 144457.3# show only coefs different from 0
out=glmnet(x,y,alpha=1,lambda=grid)
lasso_best=predict(out,type="coefficients",s=bestlam,alpha=1)[1:20,]
lasso_best[lasso_best!=0]## (Intercept) AtBat Hits Walks Years
## 48.80107051 -0.67774237 3.75024484 3.14969177 -4.59912214
## CHmRun CRuns CRBI CWalks LeagueN
## 0.16726718 0.37005850 0.41962226 -0.16768313 26.82180577
## DivisionW PutOuts Assists Errors
## -118.53979587 0.24922460 0.01431651 -0.72474528Let’s compare the different parameters
rrf = rbind(ridge_best,lasso_best)PCA
pca = prcomp(Hitters[,c('AtBat','Hits','HmRun','Runs','RBI','Walks','Years','CAtBat','CHits','CHmRun','CRuns','CRBI','CWalks','PutOuts','Assists','Errors')])
X = as.matrix(Hitters[,c('AtBat','Hits','HmRun','Runs','RBI','Walks','Years','CAtBat','CHits','CHmRun','CRuns','CRBI','CWalks','PutOuts','Assists','Errors')])
ee = eigen(t(X)%*%X)
set.seed(1)
A <- rnorm(500)
B <- -1*A
C <- 0.2*B -1.5*A
pts <- cbind(X=rnorm(500,A,.05),Y=rnorm(500,B,.05),Z=rnorm(500,C,.05))
pca2 = prcomp(pts)Kmeans
library(tripack)
library(RColorBrewer)
set.seed(1)
pts <- cbind(X=rnorm(500,rep(seq(1,9,by=2)/10,100),.022),Y=rnorm(500,.5,.15))
plot(pts)
km1 <- kmeans(pts, centers=5, nstart = 1, algorithm = "Lloyd",iter.max = 200)
CL5 <- brewer.pal(5, "Pastel1")
V <- voronoi.mosaic(km1$centers[,1],km1$centers[,2])
P <- voronoi.polygons(V)
plot(pts,pch=19,xlim=0:1,ylim=0:1,xlab="",ylab="",col=CL5[km1$cluster])
points(km1$centers[,1],km1$centers[,2],pch=3,cex=1.5,lwd=2)
plot(V,add=TRUE)
set.seed(1)
A <- c(rep(.2,100),rep(.2,100),rep(.5,100),rep(.8,100),rep(.8,100))
B <- c(rep(.2,100),rep(.8,100),rep(.5,100),rep(.2,100),rep(.8,100))
pts <- cbind(X=rnorm(500,A,.075),Y=rnorm(500,B,.075))The nice thing about k-mean is that it will adapt to the complexitiy of the problem
set.seed(1)
A <- runif(500)
B <- 0.5*A^10
pts <- cbind(X=rnorm(500,A,.05),Y=rnorm(500,B,.05))
km1 <- kmeans(pts, centers=5, nstart = 1, algorithm = "Lloyd",iter.max = 200)
CL5 <- brewer.pal(5, "Pastel1")
V <- voronoi.mosaic(km1$centers[,1],km1$centers[,2])
P <- voronoi.polygons(V)
plot(pts,pch=19,xlab="",ylab="",col=CL5[km1$cluster])
points(km1$centers[,1],km1$centers[,2],pch=3,cex=1.5,lwd=2)
plot(V,add=TRUE)