Bootstrap
Simple Lab on studying bootstrap
require(ggplot2)## Loading required package: ggplot2require(data.table)## Loading required package: data.tablerequire(reshape2)## Loading required package: reshape2##
## Attaching package: 'reshape2'## The following objects are masked from 'package:data.table':
##
## dcast, meltrequire(foreach)## Loading required package: foreachrequire(MASS)## Loading required package: MASSrequire(stringr)## Loading required package: stringrlibrary(glmnet)## Loading required package: Matrix## Loaded glmnet 4.1-6# let's consider a simple duration model
lambda = 0.01
n = 10
rr = data.table(foreach (i = 1:1000,.combine=rbind) %do% {
D = rexp(n,lambda)
res = data.frame(value=1/mean(D),value0=lambda)
res$rep = i
res$name = rownames(res)
res
})
ggplot(rr,aes(x=value)) + geom_density(fill="blue",alpha=0.2,color="blue") + geom_vline(xintercept=lambda,linetype=2,color="red") + geom_vline(xintercept=rr[,mean(value)],linetype=2,color="blue")+theme_bw()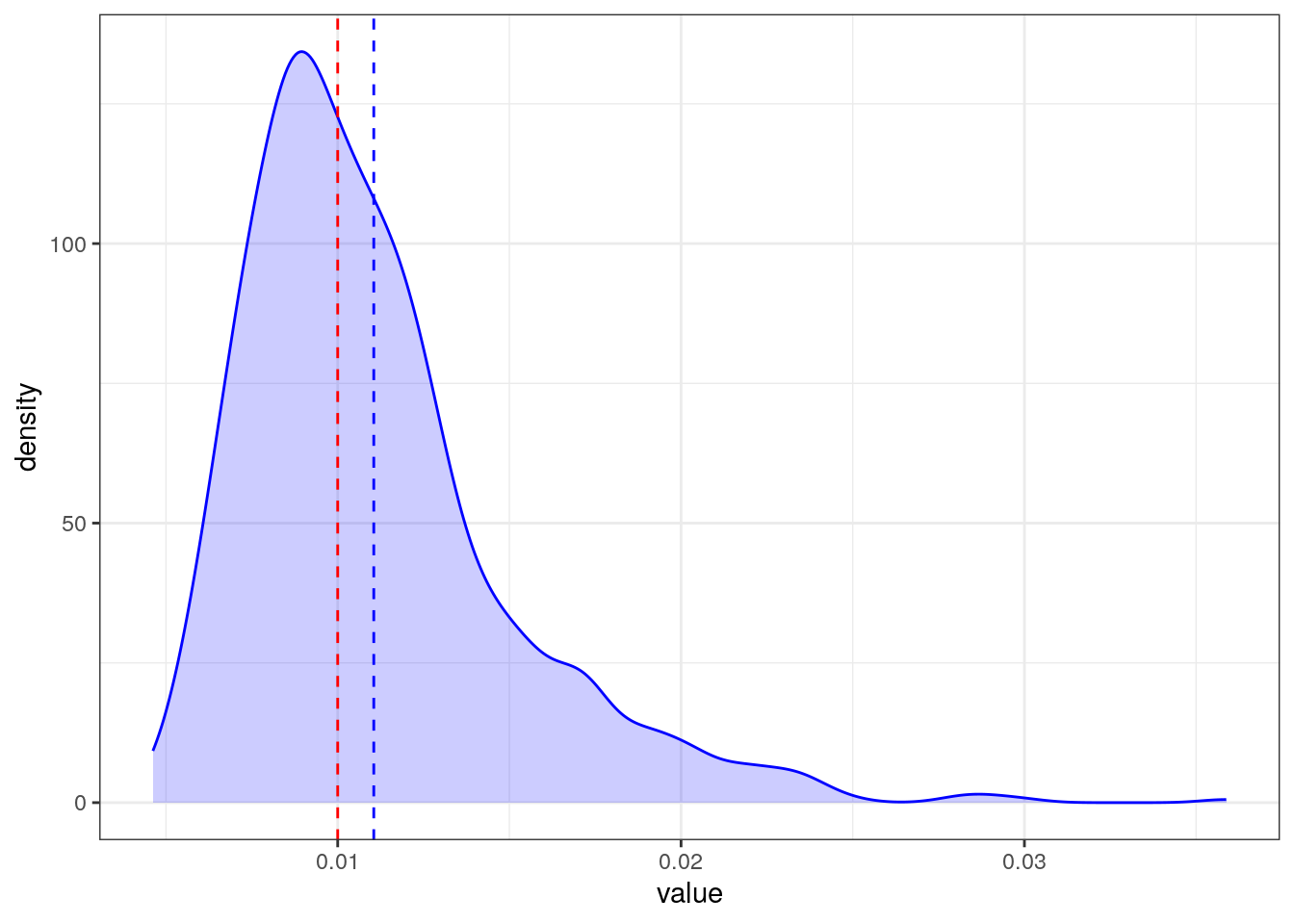
Compare bootstrap distribution to asymptotic one
We know that the asymptotic variance is \(\lambda^2\) so we can compare the asymptotic distribution approximation to bootstrap distribution.
D0 = rexp(n,lambda)
boostest <- function(D) {
# we drawn from D with replacement
D2 = sample(D,size = n,replace = TRUE)
return(1/mean(D2))
}
rr = data.table(foreach (i = 1:1000,.combine=rbind) %do% {
D = rexp(n,lambda)
res = data.frame(value=1/mean(D),value0=lambda)
res$rep = i
res$name = rownames(res)
res
})
rr[,valueb := boostest(D0),rep]
rr[,valuea := lambda + 1/sqrt(n) * lambda * rnorm(.N)]
ggplot(rr,aes(x=(value-lambda)/lambda)) + geom_density(fill="blue",alpha=0.2,color="blue") +
geom_density(aes(x=(valueb-lambda)/lambda),fill="red",alpha=0.2,color="red") +
geom_density(aes(x=(valuea-lambda)/lambda),fill="green",alpha=0.2,color="green") +
geom_vline(xintercept=lambda,linetype=2,color="red") +
theme_bw()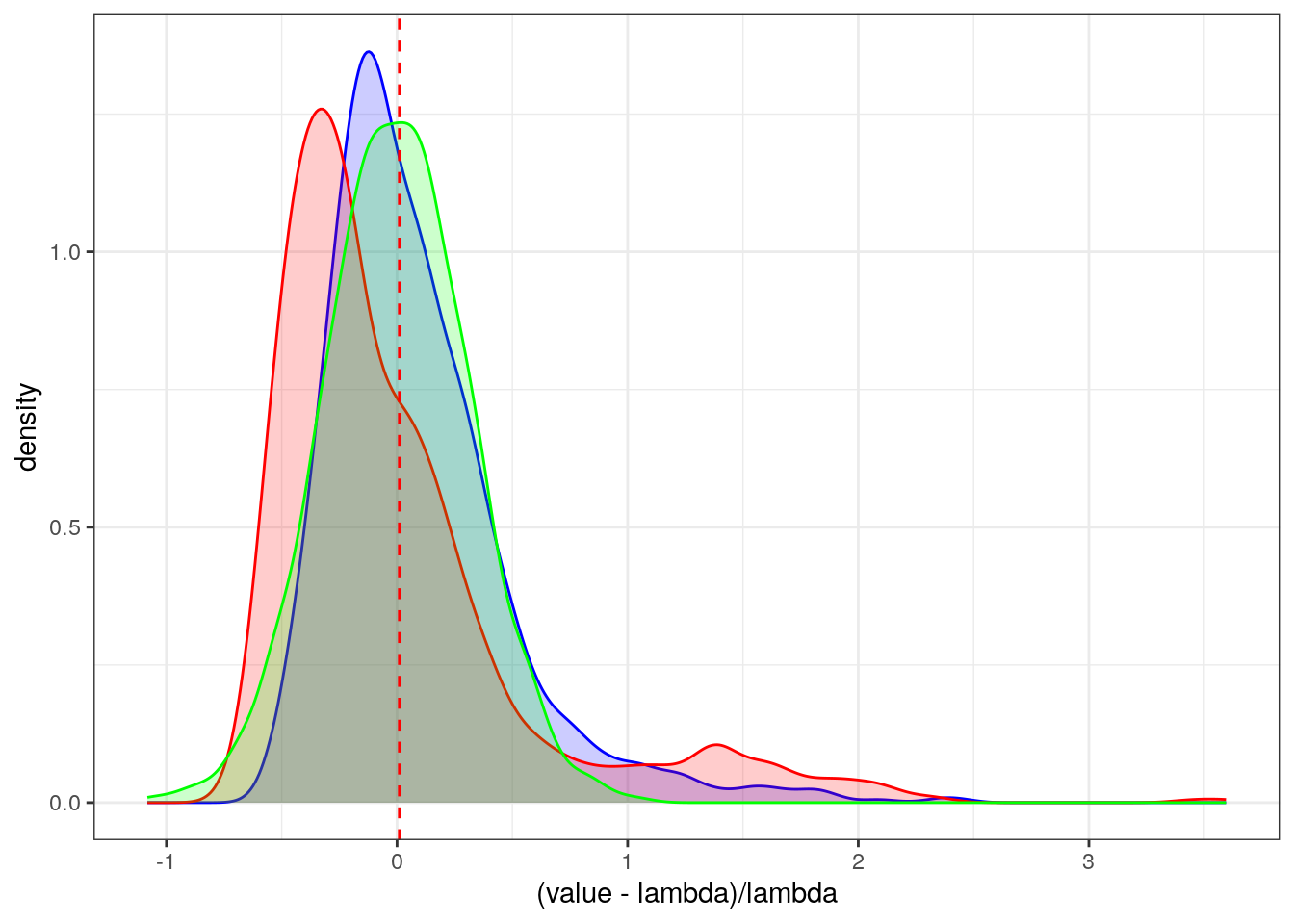
ggplot(rr,aes(x=(value))) + geom_density(fill="blue",alpha=0.2,color="blue") +
geom_density(aes(x=(valueb)),fill="red",alpha=0.2,color="red") +
geom_density(aes(x=(valuea)),fill="green",alpha=0.2,color="green") +
geom_vline(xintercept=lambda,linetype=2,color="red") +
theme_bw()
bootstrapping each time
boostest <- function(D) {
# we drawn from D with replacement
D2 = sample(D,size = n,replace = TRUE)
return(1/mean(D2))
}
rr = data.table(foreach (i = 1:5000,.combine=rbind) %do% {
D = rexp(n,lambda)
valueb = rep(0,200)
# compute bootstrap estimates
for (j in 1:200) {
valueb[j] = boostest(D)
}
res = data.frame(value=1/mean(D),value0=lambda,valueb=mean(valueb),valuesd=sd(valueb))
res$rep = i
res$name = rownames(res)
res
})
rr[,valuea := lambda + 1/sqrt(n) * lambda * rnorm(.N)]
ggplot(rr,aes(x=value)) + geom_density(fill="blue",alpha=0.2,color="blue") + geom_density(aes(x=valuea),fill="red",alpha=0.2,color="red") +
geom_density(aes(x=valueb),fill="green",alpha=0.2,color="green") +
geom_vline(xintercept=lambda,linetype=2,color="red") + geom_vline(xintercept=rr[,mean(value)],linetype=2,color="blue")+
geom_vline(xintercept=rr[,mean(valueb)],linetype=2,color="green")+
geom_vline(xintercept=rr[,2*mean(value) - mean(valueb)],linetype=1,color="orange")+theme_bw()
Extract and compare standard errors
# check a simple test that lambda is not zero
rr[,mean( abs(value-value0)<1.96*valuesd )]## [1] 0.9298rr[,mean( abs(valuea-value0)<1.96*valuesd )]## [1] 0.9222